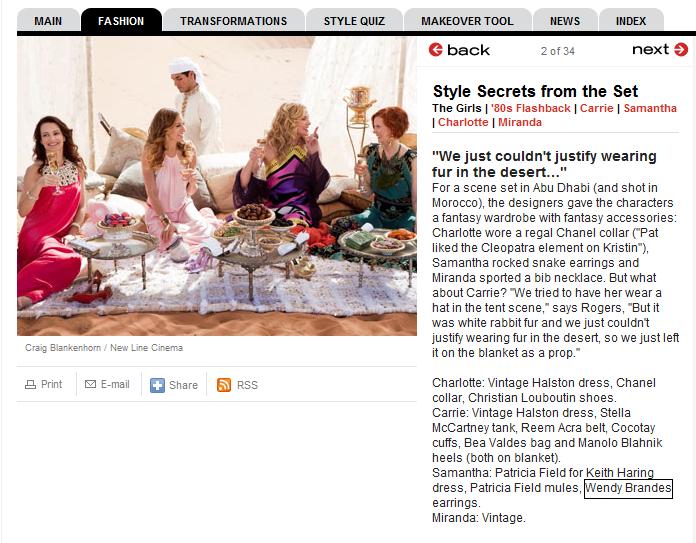
Thanks to gorgeous blogger Deja Pseu for spotting my name in an InStyle.com feature on Sex and the City 2.
For more about the earrings Samantha is wearing rather invisibly in this photo, click here, here and here.
Don’t forget that you can win a pair of the earrings in silver — worth $450 — by entering my Polyvore contest.
My pleasure!
YAY Wendy!!! wonderful! congratulations beautiful!
Oh and they were oh so perfect for the desert decadent glam scene!
xx
marian
p.s my anti-spam word is ‘finland’ hehe
I saw that, too! Those earrings are famous, Wendy! Congratulations =D
It’s very exciting that THE Samantha Jones is wearing your earrings.
Word is getting around!
Woooow, so exciting for you!
By the way, I entered your competition under my real name, not blog name, just so you know I HAVE entered 🙂 xxxx
People are coming up with such amazing ideas. It’s going to be very hard to choose.
I agree, I do not envy your task one bit.
hooray! i saw them on page 61 of US Weekly and I swear they commanded the page. I don’t think I am going to pay any attention to the movie when it comes out-I am just going to be looking for the earrings.
smiles,
gina
awesome publicity! she looks great in them
You’re taking over the world!!
Congratulations! You’re getting some really great recognition!
Heck to the freakin’ yeah! I can’t wait to see those babies on the big screen!
OMG how cool!!!!
Gosh! Congrats! That’s awesome!
Congratulations…your earings are gorgeous. Yes please…..xv
Congrats, darling!
They are fabulous!!
xoxox,
CC
happy monday sweetie pie!!
xoxo
marian.
this is so rad! you must be stoked beyond belief!
2 die 4 !!!
I can’t wait to see this film. I will definitely be looking out for your earrings.
I’m going to do the contest. Maybe. If I have a spare minute in between packing. Which I obviously do, because I decided to spend the last half hour reading blogs instead of attempting to clean.
Well hello there to you too! (And well done btw – HURRAH!)